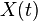Sebbene sappiamo che le performance future non siano del tutto prevedibili a partire dai risultati ottenuti in passato, possiamo dire che nella fase di test di un piano di trading ci sono alcuni aspetti che possono indicarci se, e in che misura, il nostro trading plan sia vincente o meno. Stiamo parlando di Backtesting e Forward performance testing.
Come funziona il backtesting
Nel backtesting, il primo passo consiste nel selezionare le date soglia all'interno di un periodo di tempo coperto dai dati storici. Nell'immagine qui sotto, le date soglia sono indicate come T1, T2, T3 e T4.
Quindi, per ogni data soglia,
Quindi, per ogni data soglia,
- i dati storici vengono troncati alla soglia,
- il modello di previsione è addestrato e applicato ai dati troncati,
- le previsioni così ottenute sono messe a confronto con i dati originali completi.
Infine, viene stabilito un errore medio di previsione per tutte le soglie.
Questo errore può essere interpretato come una stima dell'errore che sarà associato al modello durante l'elaborazione di previsioni vere e proprie (relative a dati futuri). Scegliere le date soglia più adeguate richiede un minimo di conoscenze in materia. Di norma, aumentare il numero delle date soglia migliora la resistenza ai problemi di overfitting.
Nel caso dell'ottimizzazione delle scorte, poiché le SKU da analizzare sono centinaia, bastano poche date soglia per decidere, con certezza quasi assoluta, se un metodo di previsione è migliore degli altri.
Un errore comune: un solo addestramento per molte previsioni
Il backtesting è generalmente un procedimento piuttosto intenso in termini di potenza di calcolo, poiché un nuovo modello di previsione deve essere addestrato per ogni soglia. Un errore che osserviamo di frequente, quindi, è addestrare il modello di previsione una volta sola, sfruttando di solito tutti i dati storici a disposizione, per poi passare direttamente al backtesting. In questo modo, si ha l'impressione di velocizzare l'intero procedimento di backtesting.
Sottolineiamo si ha l'impressione, perché in realtà un approccio del genere può causare seri problemi di overfitting. Facciamo un ragionamento implicito: se i dati futuri sono messi a disposizione del modello di previsione, il modello, indipendentemente dalla variabile da prevedere durante la fase di addestramento, includerà inevitabilmente alcune informazioni su questo futuro. Di conseguenza, l'accuratezza misurata con il backtesting non rifletterà le capacità di generalizzazione del modello, ma le capacità di memorizzazione del modello, ossia la capacità di riprodurre situazioni identiche a quelle trovate nel set di dati usato per l'addestramento.
Sottolineiamo si ha l'impressione, perché in realtà un approccio del genere può causare seri problemi di overfitting. Facciamo un ragionamento implicito: se i dati futuri sono messi a disposizione del modello di previsione, il modello, indipendentemente dalla variabile da prevedere durante la fase di addestramento, includerà inevitabilmente alcune informazioni su questo futuro. Di conseguenza, l'accuratezza misurata con il backtesting non rifletterà le capacità di generalizzazione del modello, ma le capacità di memorizzazione del modello, ossia la capacità di riprodurre situazioni identiche a quelle trovate nel set di dati usato per l'addestramento.
"I trader che sono desiderosi di provare un'idea negoziazioni in un mercato vivo spesso fanno l'errore di affidarsi interamente su di backtesting risultati per determinare se il sistema sarà redditizio"
Come funziona il Forward performance testing.
E' un test delle prestazioni in avanti fornisce i trader con un'altra serie di out-of-sample di dati su cui valutare un sistema. Il test delle prestazioni di andata è una simulazione di trading reale e coinvolge seguendo la logica del sistema in un mercato dal vivo. E 'chiamata anche di scambio di carta in quanto tutte le operazioni vengono eseguite solo su carta; cioè, le entrate commerciali e le uscite sono documentate insieme a qualsiasi utile o perdita per il sistema, ma vengono eseguiti reali compravendite. Un aspetto importante del test delle prestazioni in avanti è di seguire la logica del sistema esattamente; altrimenti, diventa difficile, se non impossibile, valutare con precisione questa fase del processo. Gli operatori dovrebbero essere onesti circa le voci del commercio e le uscite ed evitare comportamenti come cherry picking commerci o meno compreso un commercio su carta razionalizzazione che "non avrei mai preso che il commercio." Se il commercio sarebbe verificato seguente logica del sistema, deve essere documentata e valutata.
Molti broker offrono un conto di trading simulato in cui i commerci possono essere posizionati e il conto economico relativo calcolo. Utilizzando un conto di trading simulato in grado di creare un ambiente semi-realistico in cui praticare il commercio e valutare ulteriormente il sistema.
La figura 2 mostra anche i risultati di test delle prestazioni in avanti su due sistemi. Anche in questo caso, il sistema rappresentato nella tabella sinistra non riesce a fare ben oltre i test iniziali sui dati in-campione. Il sistema mostrato nel grafico a destra, tuttavia, continua a funzionare bene in tutte le fasi, compresa la prova di prestazione avanti. Un sistema che mostra risultati positivi con buona correlazione tra in-campione, out-of-campione e di test delle prestazioni in avanti è pronto per essere implementato in un mercato dal vivo.



 , valutata in
, valutata in 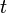 , è dato da:
, è dato da:

 è il prezzo del titolo
è il prezzo del titolo  è il
è il  è il
è il  denota la
denota la 

 non è necessariamente pari a
non è necessariamente pari a  ; tramite il
; tramite il  a quello desiderato, sfruttando il concetto di
a quello desiderato, sfruttando il concetto di  denota il prezzo dell'
denota il prezzo dell'

 è la
è la ![\ P(S,t)=e^{-r(T-t)}\textrm{E}[(K-S_{T})\mathbf{1}_{S_{T}<K}]](https://upload.wikimedia.org/math/1/3/3/133dfaf5e3725ef8c2e3ae817a105cf6.png)
![\ P(S,t)=Ke^{-r(T-t)}\textrm{E}[\mathbf{1}_{S_{T}<K}]-e^{-r(T-t)}\textrm{E}[S_{T}\mathbf{1}_{S_{T}<K}]=](https://upload.wikimedia.org/math/5/e/6/5e630f39585fe4ee7b13be7ced5b5f88.png)
![\ = Ke^{-r(T-t)}\Pr(S_{T}<K)-e^{-r(T-t)}\textrm{E}[S_{T}\mathbf{1}_{S_{T}<K}]](https://upload.wikimedia.org/math/8/b/5/8b5d052f672e2b780085ddcfa30cea67.png)

![\ e^{-r(T-t)}\textrm{E}[S_{T}\mathbf{1}_{S_{T}<K}]=e^{-r(T-t)}\textrm{E}[S_{T}|S_{T}<K]=](https://upload.wikimedia.org/math/9/f/d/9fdab205d80fc2180141148959a981ca.png)
![=S_{t}\exp\left(-\frac{1}{2}\sigma^{2}(T-t)\right)\textrm{E}[\exp\{\sigma(W_{T}-W_{t})\}|S_{T}<K]](https://upload.wikimedia.org/math/1/f/0/1f027aa7503a70555c2a0dbd7efa0d1f.png)
 ; quanto sopra equivale a voler calcolare:
; quanto sopra equivale a voler calcolare:

 ; dunque
; dunque  , e l'
, e l' ; l'espressione da calcolare risulta:
; l'espressione da calcolare risulta:

![\ [t,t+dt]](https://upload.wikimedia.org/math/f/e/5/fe5613d89c5539001482af45985f765b.png) :
:
 è una costante reale, e indica il tasso istantaneo di dividendo. Sulla base di questa formulazione, tramite un procedimento standard è possibile mostrare che il prezzo di non
è una costante reale, e indica il tasso istantaneo di dividendo. Sulla base di questa formulazione, tramite un procedimento standard è possibile mostrare che il prezzo di non