è possibile identificare un processo stocastico come una famiglia ad un parametro di variabili casuali reali
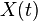rappresentanti le trasformazioni dello stato iniziale nello stato al tempo 
. In termini più precisi, un processo stocastico si basa su una variabile casuale che prende valori in spazi più generali dei numeri reali (come ad esempio, 
, o spazi funzionali, o successioni di numeri reali).Da un punto di vista pratico, un processo stocastico è una forma di rappresentazione di una grandezza che varia nel tempo in modo casuale (ad esempio un segnale elettrico, il numero di autovetture che transitano su un ponte, etc.) e con certe caratteristiche.
Definizione di MOTO BROWNIANO: si fa riferimento al moto disordinato delle particelle (aventi diametro dell'ordine del micrometro) presenti in fluidi o sospensioni fluide.
Sebbene l'osservazione di questo fenomeno da parte di Jan Ingenhousz sia avvenuta nel 1785, esso venne riscoperto nel 1828 da Robert Brown (che osservò il moto del polline in una sospensione acquosa), per poi avere una trattazione matematica rigorosa solo agli inizi del Novecento con Louis Bachelier (1900 - Théorie de la spéculation, tesi di laurea) e Albert Einstein .
Possiamo ricreare tutto ciò grazie alla programmazione in Visual Studio andando a osservare la variazione dei prezzi in un certo arco di tempo:
Nessun commento:
Posta un commento